平均値を学び直そう 統計学
こんにちはOnoです。今回は、平均値についての話です。皆さん、会社では仕事の色々な指標を出す際に平均値をよく使われると思います。一般的に平均値というとすぐに、データの総和をデータ数で割ると思いつくのではないでしょうか。データ\(\{x_1 \quad x_2···x_n\} \)の合計をデータ数\(N\)で割った物を数式で表すと平均値は下記のようになります。
$$\bar{x}=\frac{\{x_1 + x_2···x_n\}}{N}=\frac{\sum_{i=1}^N x_i}{N}$$
かくいう私も当たり前のように、平均値を使っていました。
しかし、漠然と平均値を使うと、本当のデータの特性を表していないと思う時はないでしょうか?。そこで今回は平均値について書いていきたいと思います。
まず平均値は基礎統計量のうちどこに分類されるかというと、データを代表する値(中心的傾向の特性値)に分類されます。
データを代表する値には、平均値、中央値、最頻値、トリム平均、最大値、最小値があります。
中央値はメディアン、最頻値はモードとも言います。なんとなく耳にしたことがあるかもしれません。ちなみに、平均値はミーンと言います。
実は、平均値にも色々あります。データの総数をデータ数で割るのは算術平均と呼ばれます。その他に幾何平均、二乗平均、調和平均などがあります。
今回の記事において、平均値は算術平均の事を言っています。
平均値は、計算しやすいのですが、飛び離れた値の影響を強く受けてしまいます。また多く現れるデータは平均値に与える影響が大きいという特徴があります。
さらに全データを平均値とみなみしても、全データの合計という観点からだと問題は起きないとも言えます。
そして平均値は分布の重心であるという事も言えます。データの分布を仮に実際に持てる場合、平均値の点で支えると、図1のように右にも左にも傾かないことになります。
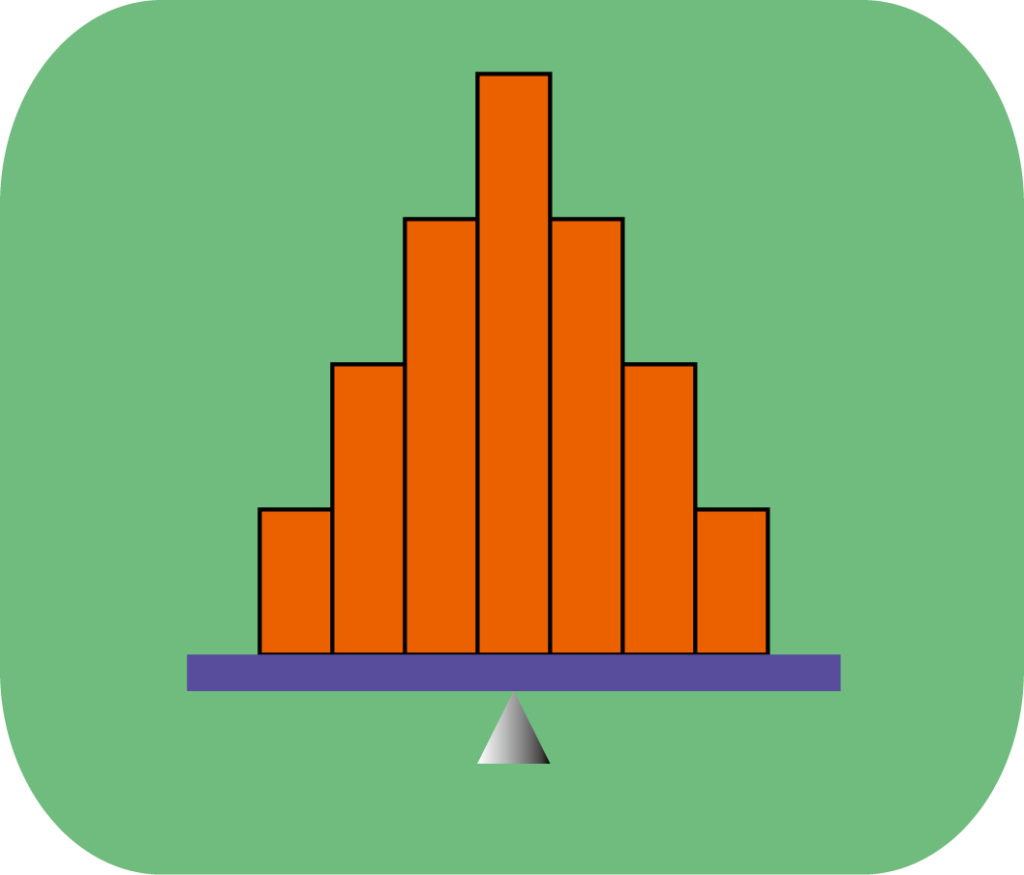
このように、平均値と一言に言ってもとても奥が深い物になっています。今回の話が実務で平均値を使う時の参考になればと思います。
最後まで、みていただいてありがとうございました。