分散　標準偏差　変動係数

今回は、分散・標準偏差・変動係数について説明していきます。

早速ですが、分散と標準偏差、変動係数を計算してみましょう。使用するデータは表１となります。

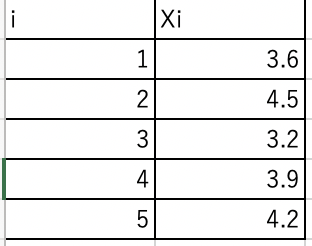
表１は、ねこの5匹の体重を観測したものになります。まずねこ5匹の体重の平均を求めます。

$\bar{X}_i=\frac{1}{n}\sum X_{i}=\frac{3.6+4.5+3.2+3.9+4.2}{5}=3.88$

分散\(s^2\)を計算します。

$s^2=\frac{1}{n-1} (\sum X_{i}^2-\bar{X}•\sum X_i)$

ここで、\(\sum X_i^2\)は体重を2乗したものを足し合わせます。よって

$\sum X_i^2=(3.6^2+4.5^2+3.2^2+3.9^2+4.2^2)=76.3$

また\(\sum X_i\)は体重の総和なので、

$\sum X_i =(3.6+4.5+3.2+3.9+4.2)=19.4$

したがって分散\(s^2\)は

$s^2=\frac{1}{5-1}(76.3-3.88×19.4)=0.257$

となり、標準偏差\(s\)は

$s=0.507$

となります。また変動係数は\(C=\frac{s}{\bar{X}}\)と表すことができ、標準偏差をねこの体重の平均で割った値になっています。したがって、

$C=\frac{0.507}{3.88}=0.131$

となります。ここまで計算してみて、実際に求めた物が何を意味するかですが、偏差\(s\)は標本データ（ねこ5匹の体重）の変動を平均からの偏差（\(各データの値ー平均値\)）とすると、標準的に\(0.507kg\)となることを意味します。

変動係数は、全く異なる動物である（例えば）イヌと、体重の散らばりの程度を比較しようとするときに利用することができます。例えば、イヌ5匹の体重の標本平均\(\bar{X}=11.5Kg\)、標準偏差が、\(s=0.810\)だとすると、

$C=\frac{0.810}{11.5}=0.070$

となります。そして変動係数は標準偏差が平均の何倍であるかを示しています。つまり

(1)ねこ5匹の体重の標準偏差は、平均体重の0.131倍
(2)イヌ5匹の体重の標準偏差は、平均体重の0.070倍

になることがわかります。よって変動係数によって異なる標本の変動を比較するのに利用することができます。

今回は分散、標準偏差、変動係数について説明しました。今回の記事が皆様のデータを見る際のお役に立てれば幸いです。