サクッと確率分布-統計学-
さて今回は、統計学における確率分布に関するお話です。確率分布なんて聞くと難しそうなイメージがしますが、怖がらずに挑戦してみましょう。
今回の例として、137人の靴のサイズの相対度数分布の図を下記に示します。
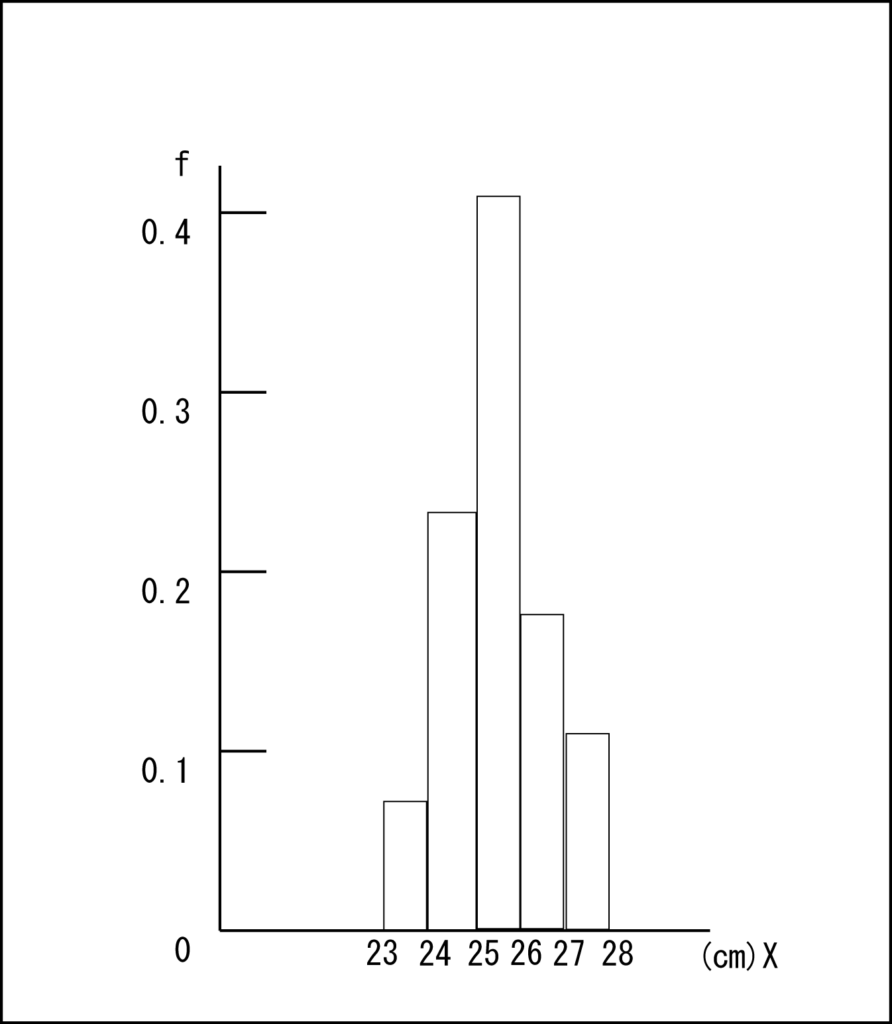
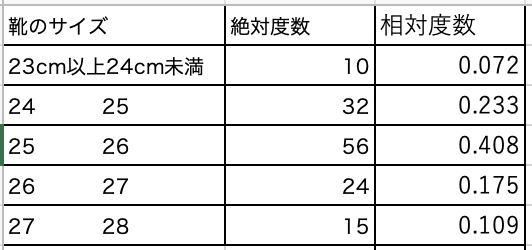
図2の靴のサイズ毎の相対度数をグラフにしたのが、図1になります。
図1、図2より「23cm以上24cm未満」の靴のサイズの相対度数は0.072と読み取れるので、統計学では下記(1)のように表します。
(1) f ( 23 ≦ X < 24 ) = 0.072
(Xが23以上24未満であるという現象の相対度数fは0.072)
また、「25cm以上26cm未満」の靴のサイズの相対度数は0.408なので、同様に下記(2)のようになります。
(2) f ( 25 ≦ X < 26) = 0.408
(Xが25以上26未満であるという現象の相対度数fは0.408)
(2)を確率の記号Pを使って表すと、下記(3)のようになります。
(3) P ( 25 ≦ X < 26 ) = 0,408
(3)は「X(靴のサイズ)が25以上26未満である確率Pは0.408」ということを言っています。
統計学の考え方の特徴として、「すべての統計的現象は確率分布をする」というのがあるので、(3)をさらに踏み込んで考えると、
靴のサイズが25cm~26cmである確率は0.408であるということが、現象固有の特性であると考えます。
つまり、統計学の考え方とは、同じ条件の下で靴のサイズは確率分布をすると考える。そしてその確率分布を分析する手法を学ぶという考え方になります。
確率分布までを理解したら、いよいよ統計の分析手法を学んでいく事になります。